1. 현황
최근 삼성전자 주가가 심상치 않게 빠지고 있습니다.
국내 경제의 불확실성 증가, 삼성 내부 문제, 다른 기업들과의 기술 격차, AI 반도체(HBM) 개발 실패 문제로 인해 삼성전자의 주가는 연일 하락하고 있습니다.

현재 삼성전자 주가는 49,900원으로 5만원이 깨지면서 최근 고점(88,800원) 대비 약 43% 빠졌습니다.
2. ELS란?
ELS란 기초자산 가격의 변동에 따라 미리 정해진 수익 구조에 의해 특정 시점에 지급을 약속하는 금융 상품입니다.
기초 상품의 경우, 국내 또는 해외의 주가지수나 특정 주식 가격에 해당합니다.
ELS 상품의 예시는 다음과 같습니다. 아래 상품은 KB에서 실제로 판매했던 상품입니다.




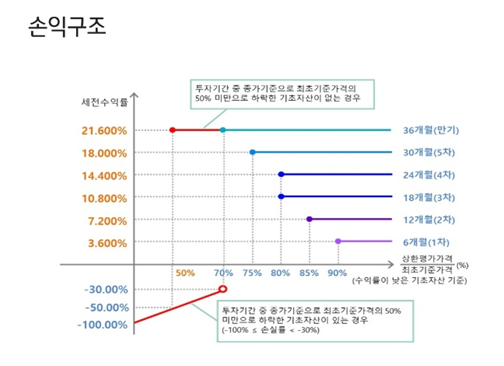
위 상품과 같이 최초기준가격의 50% 미만으로 주가가 하락한다면, 조건이 발동되게 됩니다.
조건이 발동되면 -50% 손실부터 시작하게 됩니다. 주가가 다시 상승하더라도 -30%까지 손해를 보게 됩니다.
물론 그 이상으로 기준가에 70% 이상의 가격이 회복한다면 손실 조건이 풀리게 됩니다.
주가가 추가적으로 하락하게 되면 그만큼 손실은 이어지게 됩니다.
그리고 각 시기마다 조기 상환할 수 있는 가격이 정해져 있습니다.
당연하게도 주가가 50% 이상 빠지는 일은 드뭅니다. 그런 일이 일반적으로 일어나지 않습니다.
하지만, 비교적 최근 홍콩 ELS 사태와 마찬가지로 일어나지 않는다는 생각은 위험합니다.
위 상품의 경우, 2024년 1월 19일 삼성전자 종가는 74,700원였습니다. 손실 발동 조건은 이에 50%인 37,350원이 되게 됩니다. 현재 종가 49,900원에 비해 한참 낮은 가격입니다. 그러한 점에서 이 상품의 손실 가능성은 낮다고 평가할 수 있습니다.
하지만, 청약 시기에 따라 큰 손실이 발생할 수 있는 위험 가능성이 존재합니다.
지난 24년 8월 LG 화학과 인텔이 폭락하면서 KB able ELS 제3109호를 비롯해 많은 ELS 상품들이 손실 구간으로 들어가게 되었습니다.
청약식으로 투자하는 ELS 상품, 안전하게 일정 금액을 취할 수 있다는 점에서 횡보장에 매력적인 상품이지만, 이런 상황에 놓이게 되면 크게 손실을 볼 수 있는 위험이 존재합니다.
3. ELS 상품의 운용 방식

원금비보장형 ELS는 투자 초기부터 높은 수익을 추구하는 운용 방식을 취합니다.
안전자산인 채권 비중을 낮게 가져가는 대신, 주식, 선물, 옵션 등 고위험 자산의 비중을 높게 가져갑니다.
이러한 운용 방식은 높은 수익을 얻을 수 있는 가능성을 제공하지만, 동시에 원금 손실 위험도 크다는 특징이 있습니다. 특히 선물과 옵션 투자의 성과가 전체 수익에 큰 영향을 미치며, 이러한 투자 위험은 발행 증권사가 부담하게 됩니다.
일반 펀드와 달리 ELS는 운용실패의 위험을 투자자가 아닌 발행 증권사가 부담하기 때문에, 증권사의 수익성에도 큰 영향을 미칠 수 있습니다.
이에 대응하기 위해 큰 폭의 손실은 투자자도 같이 부담하도록 설계한 것입니다.
4. ELS 가격 결정 모형
AI에게 ELS에게 한 번 물어봤는데 이러한 답변을 받았습니다. 이정도까지 학습이 되었다는게 또 새삼 놀랍네요.
import numpy as np
import pandas as pd
from scipy.stats import norm
import matplotlib.pyplot as plt
class ELSDesigner:
def __init__(self, underlying_price, volatility, risk_free_rate, dividend_yield, maturity):
"""
ELS 상품 설계를 위한 기본 파라미터 초기화
Parameters:
- underlying_price: 기초자산의 현재가격
- volatility: 기초자산의 변동성 (연간)
- risk_free_rate: 무위험 이자율 (연간)
- dividend_yield: 배당수익률 (연간)
- maturity: 만기 (년)
"""
self.S0 = underlying_price
self.vol = volatility
self.r = risk_free_rate
self.q = dividend_yield
self.T = maturity
def simulate_paths(self, n_paths, n_steps):
"""
Black-Scholes 모형 가정 하에 기초자산 가격 경로를 시뮬레이션
Parameters:
- n_paths: 시뮬레이션할 경로 수
- n_steps: 시간 구간 분할 수 (보통 trading days = 252 사용)
Returns:
- paths: (n_paths, n_steps+1) 크기의 가격경로 배열
"""
# 시간 간격 계산
dt = self.T / n_steps
# Black-Scholes 드리프트와 확산항 계산
drift = (self.r - self.q - 0.5 * self.vol**2) * dt # risk-neutral measure 하의 drift
diffusion = self.vol * np.sqrt(dt) # 확산항 (변동성)
# 가격경로 배열 초기화
paths = np.zeros((n_paths, n_steps + 1))
paths[:, 0] = self.S0 # 초기가격 설정
# 기하브라운운동을 통한 가격경로 생성
for t in range(1, n_steps + 1):
z = np.random.standard_normal(n_paths) # 표준정규분포 난수 생성
paths[:, t] = paths[:, t-1] * np.exp(drift + diffusion * z)
return paths
def calculate_payoff(self, paths, knock_in_barrier, knock_out_barriers,
coupon_rates, observation_dates, n_steps):
"""
각 경로별 ELS 페이오프 계산
Parameters:
- paths: 시뮬레이션된 가격경로들
- knock_in_barrier: 원금손실 발생 배리어
- knock_out_barriers: 각 관찰일의 조기상환 배리어 리스트
- coupon_rates: 각 관찰일의 쿠폰 수익률 리스트
- observation_dates: 관찰일 리스트 (년)
- n_steps: 시간 구간 분할 수
Returns:
- payoffs: 각 경로별 최종 페이오프
"""
n_paths = len(paths)
payoffs = np.zeros(n_paths) # 페이오프 배열 초기화
knocked_out = np.zeros(n_paths, dtype=bool) # 조기상환 여부 추적
# 각 관찰일별 조기상환 조건 체크
for i, barrier in enumerate(knock_out_barriers):
# 관찰일을 시뮬레이션 스텝으로 변환
obs_date = min(int(observation_dates[i] / self.T * n_steps), n_steps)
# 조기상환 조건 체크 (기초자산가격 >= 배리어 수준)
condition = paths[:, obs_date] >= barrier * self.S0
# 아직 조기상환되지 않은 경로 중 조건 만족하는 경로 처리
current_knockouts = condition & ~knocked_out
if np.any(current_knockouts):
payoffs[current_knockouts] = (1 + coupon_rates[i]) # 원금 + 쿠폰
knocked_out = knocked_out | current_knockouts
# 만기까지 조기상환되지 않은 경로 처리
not_knocked_out = ~knocked_out
if np.any(not_knocked_out):
# 녹인 여부 확인 (경로 중 최저가격이 녹인배리어 미만)
knock_in_mask = np.min(paths[not_knocked_out], axis=1) < knock_in_barrier * self.S0
knock_in_indices = np.where(not_knocked_out)[0][knock_in_mask]
# 녹인된 경우: 만기 기초자산 가격 비율만큼 원금 지급
if len(knock_in_indices) > 0:
payoffs[knock_in_indices] = np.minimum(
paths[knock_in_indices, -1] / self.S0,
1.0
)
# 녹인되지 않은 경우: 원금 100% + 쿠폰 지급
no_knock_in_indices = np.where(not_knocked_out)[0][~knock_in_mask]
if len(no_knock_in_indices) > 0:
payoffs[no_knock_in_indices] = 1.0 + + coupon_rates[-1]
return payoffs
def price_els(self, n_paths=10000, n_steps=252):
"""
몬테카를로 시뮬레이션을 통한 ELS 가격 산출
Parameters:
- n_paths: 시뮬레이션 경로 수
- n_steps: 시간 구간 분할 수
Returns:
- price: ELS 현재가치
- paths: 시뮬레이션된 가격경로들
"""
# 상품구조 정의
knock_in_barrier = 0.6 # 원금손실 배리어 (60%)
knock_out_barriers = [0.95, 0.95, 0.90, 0.90, 0.85, 0.85] # 조기상환 배리어
coupon_rates = [0.07, 0.14, 0.21, 0.28, 0.35, 0.42] # 쿠폰 수익률
observation_dates = [0.5, 1.0, 1.5, 2.0, 2.5, 3.0] # 관찰일 (6개월 간격)
# 가격경로 시뮬레이션
paths = self.simulate_paths(n_paths, n_steps)
# 페이오프 계산
payoffs = self.calculate_payoff(paths, knock_in_barrier, knock_out_barriers,
coupon_rates, observation_dates, n_steps)
# 무위험이자율로 현재가치 할인
price = np.exp(-self.r * self.T) * np.mean(payoffs)
return price, paths
# 테스트 코드
els = ELSDesigner(
underlying_price=100, # 기초자산 현재가 100
volatility=0.2, # 연간 변동성 20%
risk_free_rate=0.03, # 연간 무위험이자율 3%
dividend_yield=0.01, # 연간 배당수익률 1%
maturity=3.0 # 만기 3년
)
# ELS 가격 계산 및 시뮬레이션 결과 시각화
price, paths = els.price_els()
print(f"ELS 가격: {price:.4f}")
# 첫 5개 경로만 플롯
plt.figure(figsize=(10, 6))
plt.plot(paths[:5].T)
plt.title("Underlying asset price path simulation")
plt.xlabel("time")
plt.ylabel("price")
plt.grid(True)
plt.show()
- simulate_paths():
- 표준정규분포 난수로 주가 경로 생성
- 각 경로는 3년간 252거래일의 주가를 표현
- Black-Scholes 모형 기반 - calculate_payoff():
- 각 관찰일(6개월마다)에 녹아웃 조건(95%, 90%, 85%) 체크
- 조건 달성시: 원금 + 해당 차수 쿠폰
- 만기까지 달성 실패시:
- 녹인(60%) 발생: 만기주가/기초주가 비율로 원금 지급
- 녹인 미발생: 원금 + 마지막 쿠폰(42%) 지급 - price_els():
- 10,000개 경로 시뮬레이션
- 각 경로의 페이오프 평균
- 무위험이자율로 현재가치 할인
결과
ELS 가격: 0.9914
* 이 상품의 이론적 가치는 액면가의 99.14%라는 뜻
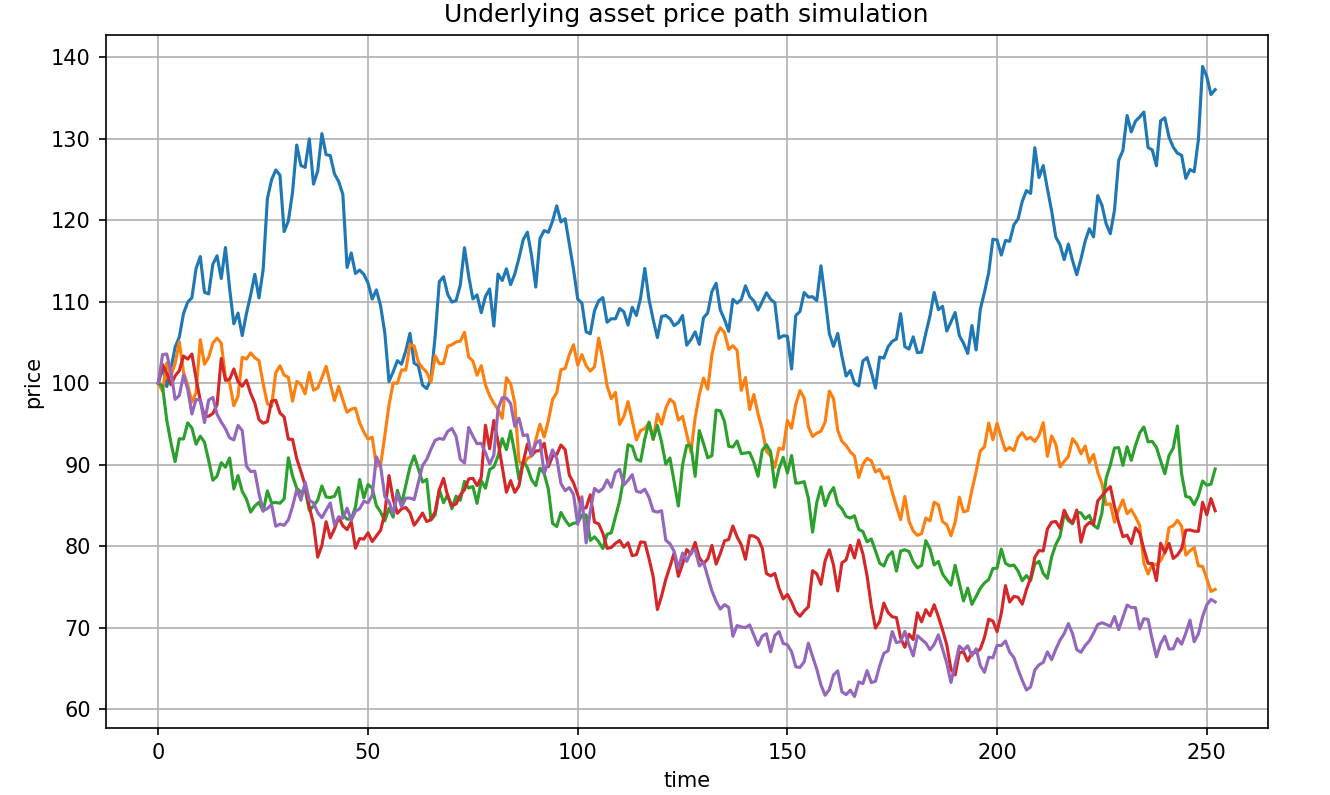
몬테카를로 시뮬레이션은 표준정규분포를 따르기 때문에
주가가 로그표준정규분포(수익률 계산이기 때문)를 따르게 됩니다.
'경제 이야기' 카테고리의 다른 글
| 미국 금리 추이 변화 (3) | 2024.11.16 |
|---|---|
| 금융사 리스크 관리 (1) | 2024.11.15 |
| KDI 2025년 국내 경제전망(2) (0) | 2024.11.14 |
| KDI 2025년 국내 경제전망(1) (2) | 2024.11.13 |
| 대출 규제에 따른 '풍선 효과' 발생 (4) | 2024.11.11 |



